Skip to main content

公式

乘方运算​

am⋅an=am+na^m ⋅ a^n = a^{m + n}
aman=am−n\frac{a^m}{a^n} = a^{m-n}
(ab)n=an⋅bn(ab)^n = a^n ⋅ b^n
(ab)n=anbn(\frac{a}{b})^n = \frac{a^n}{b^n}
(am)n=amn(a^m)^n = a^{mn}
a≠0a \ne 0 时，a0=1a^0 = 1，a−n=1ana^{-n} = \frac{1}{a^n}

开方运算​

anma^{\frac{n}{m}} = anm\sqrt[m]{a^n}
abn\sqrt[n]{ab} = an⋅bn\sqrt[n]{a} ⋅ \sqrt[n]{b}
abn\sqrt[n]{\frac{a}{b}} = anbn\frac{\sqrt[n]{a}}{\sqrt[n]{b}}

公式​

(a+b)(a−b)=a2−b2(a + b)(a - b) = a^2 - b^2（平方差公式）
(a+b)2=a2+2ab+b2(a + b)^2 = a^2 + 2ab + b^2（完全平方公式）
(a−b)2=a2−2ab+b2(a - b)^2 = a^2 - 2ab + b^2（完全平方公式）
(a+b)3=a3+b3+3a2b+3ab2(a + b)^3 = a^3 + b^3 + 3a^2b + 3ab^2
(a−b)3=a3−b3−3a2b+3ab2(a - b)^3 = a^3 - b^3 - 3a^2b + 3ab^2
a3+b3=(a+b)(a2−ab+b2)a^3 + b^3 = (a + b)(a^2 - ab + b^2)
a3−b3=(a−b)(a2+ab+b2)a^3 - b^3 = (a - b)(a^2 + ab + b^2)

一元二次方程的求根公式​

ax2+bx+c=0ax^2 + bx +c = 0
x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}

韦达定理​

x1x_1 和 x2x_2 是方程 ax2+bx+c=0ax^2 + bx + c = 0 的两个根，则有：
x1+x2=−bax_1 + x_2 = -\frac{b}{a}
x1⋅x2=cax_1 \cdot x_2 = \frac{c}{a}

均值不等式​

两个正数的均值不等式是：a+b≥2aba + b ≥ 2\sqrt{ab}，当且仅当 a = b 时取等号。
三个正数的均值不等式是：a+b+c≥3abc3a + b + c ≥ 3\sqrt[3]{abc}，当且仅当 a = b = c 时取等号。
n 个正数的均值不等式是：a1+a2+⋯+an≥na1a2…anna_1 + a_2 + \dots + a_n ≥ n\sqrt[n]{a_1a_2 \dots a_n}，当且仅当 a1=a2=⋯=ana_1 = a_2 = \dots = a_n 时取等号。

等差数列​

通项公式：an=a1+(n−1)da_n = a_1 + (n - 1)d
前 n 项和公式：Sn=n(a1+an)2S_n = \frac{n(a_1 + a_n)}{2}

等比数列​

通项公式：an=a1qn−1a_n = a_1q^{n-1}
前 n 项和公式：
当 q = 1 时，Sn=na1S_n = na_1
当 q ≠\ne 1 时，sn=a1(1−qn)1−qs_n = \frac{a_1(1 - q^n)}{1 - q}

排列数​

Pnm=n(n−1)(n−2)⋅⋯⋅(n−m+1)P_n^m = n(n - 1)(n - 2) \cdot \cdots \cdot (n - m + 1)
当 m = n 时，Pnm=n(n−1)(n−2)⋅⋯⋅2⋅1P_n^m = n(n - 1)(n - 2) \cdot \cdots \cdot 2 \cdot 1， 称为 n 的全排列。
PnnP_n^n = n!，n! 读作 n 的阶乘。
Pnm=n!(n−m)!P_n^m = \frac{n!}{(n - m)!}

组合数​

Cnm=PnmPmm=n(n−1)(n−2)⋅⋯⋅(n−m+1)m!C_n^m = \frac{P_n^m}{P_m^m} = \frac{n(n - 1)(n - 2) \cdot \cdots \cdot (n - m + 1)}{m!}
Cnn=Cn0=1C_n^n = C_n^0 = 1
Cnm=Cnn−mC_n^m = C_n^{n - m}

错位重排​

伯努利-欧拉装错信封问题 不对号入座/球的号码跟盒子不对应······

元素对数错位重排方法数
10
21
32
49
544

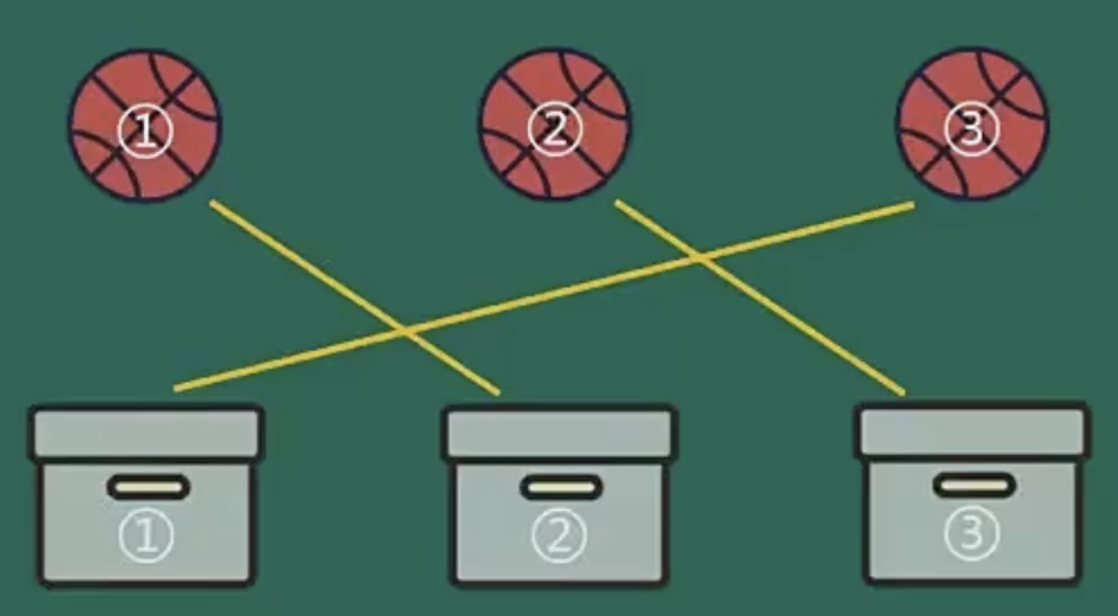
(题型定位)不对应问题 -> 错位重排

正弦定理​

对于任意一个三角形，各边和它所对角的正弦值的比相等且等于外接圆的直径。

asin⁡A=bsin⁡B=csin⁡C=2r\frac{a}{\sin{A}} = \frac{b}{\sin{B}} = \frac{c}{\sin{C}} = 2r（r为外接圆半径）

余弦定理​

对于任意三角形，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。

c2=a2+b2−2abcos⁡Cc^2 = a^2 + b^2 - 2ab\cos{C}
b2=a2+c2−2accos⁡Bb^2 = a^2 + c^2 - 2ac\cos{B}
a2=b2+c2−2bccos⁡Aa^2 = b^2 + c^2 - 2bc\cos{A}

弦切角定理​

弦切角的度数等于它所夹的弧所对的圆心角度数的一半，等于它所夹的弧所对的圆周角度数。

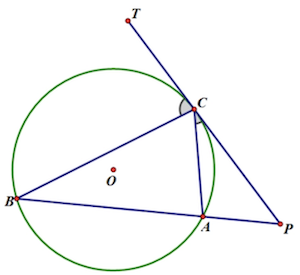
∠PCA（弦切角） = ∠ABC（圆周角）
∠TCB（弦切角） = ∠BAC（圆周角）

点到直线的距离​

点 P(x0,y0)P(x_0, y_0) 到直线 l：Ax+By+C=0Ax + By + C = 0 的距离：
d=∣Ax0+By0+C∣A2+B2d = \frac{\vert Ax_0 + By_0 + C \vert}{\sqrt{A^2 + B^2}}

两条平行直线间的距离​

两条平行直线：
l1:Ax+By+C1=0l_1: Ax + By + C_1 = 0
l2:Ax+By+C2=0l_2: Ax + By + C_2 = 0 的距离：
d=∣C1−C2∣A2+B2d = \frac{\vert C_1 - C_2 \vert}{\sqrt{A^2 + B^2}}

抛物线图像​

二次函数 y=ax2+bx+cy = ax^2 + bx + c 的图像的对称轴方程是：
x=−b2ax = -\frac{b}{2a}
顶点坐标是：
(−b2a,4ac−b24a)(-\frac{b}{2a}, \frac{4ac - b^2}{4a})

圆的方程​

圆的标准方程是：​

(x−a)2+(y−b)2=r2(x - a)^2 + (y - b)^2 = r^2
其中，圆心坐标是 (a,b)(a, b) ，半径是 r 。

圆的一般方程是：​

x2+y2+Dx+Ey+F=0 (D2+E2−4F>0)x^2 + y^2 + Dx + Ey + F = 0 \space (D^2 + E^2 -4F > 0)
其中，圆心坐标是 (−D2,−E2)(-\frac{D}{2}, -\frac{E}{2}) ，半径是 r=D2+E2−4F2r = \frac{\sqrt{D^2 + E^2 -4F}}{2} 。

圆形​

圆的周长公式：C=2πr=πdC = 2 \pi r = \pi d
圆的面积公式：S=πr2S = \pi r^2

球体​

球体表面积公式：S=4πR2S = 4 \pi R^2
球体体积公式：V=43πR3V = \frac{4}{3} \pi R^3

平均值、方差、标准差​

平均值：x‾=x1+x2+⋯+xnn\overline{x} = \frac{x_1 + x_2 + \cdots + x_n}{n}

方差：s2=(x1−x‾)2+(x2−x‾)2+⋯+(xn−x‾)2ns^2 = \frac{(x_1 -\overline{x})^2 + (x_2 - \overline{x})^2 + \cdots + (x_n - \overline{x})^2}{n}

标准差：s

其他​