Skip to main content

数据统计

第33节 加法原理​

加法原理​

如果完成一件事有 n 类办法,只要选择其中任何一类办法中的任何一种方法，就可以完成这件事。
若第一类办法中有 m1m_1 种不同的方法，
第二类办法中有 m2m_2 种不同的方法，
第 n 类办法中有 mnm_n 种不同的办法，
那么完成这件事共有 N = m1+m2+⋯+mnm_1 + m_2 + \cdots + m_n, 种不同的方法。

加法原理举例​

由 A 地到 B 地，如果乘火车，有 3 班车次；如果乘汽车，有 4 班车次；如果乘轮船，有 2 个班次。那么由 A 到 B 的方法共有多少种？
N = 3 + 4 + 2 = 9

第34节 乘法原理​

乘法原理​

如果完成一件事，必须依次连续地完成 n 个步骤，这件事才能完成。
若完成第一个步骤有 m1m_1 种不同的方法，
完成第二个步骤有 m2m_2 种不同的方法，
完成第 n 个步骤有 mnm_n 种不同的办法，
那么完成这件事共有 N = m1⋅m2⋅⋯⋅mnm_1 \cdot m_2 \cdot \cdots \cdot m_n，种不同的方法。

乘法原理举例​

由 A 地到 B 地，途中要经过 C 地换乘。如果 A 到 C 有公交车 4 个班次; C 到 B 有公交车 5 个班次；那么由 A 到 B 的乘车方法共有多少种？
N = 4 x 5 = 20

第35节 排列与排列数​

排列​

从 n 个不同元素中，任意取出 m 个元素，按照一定顺序排成一列，称为从 n 个不同元素中取出 m 个元素的一个排列。

排列数​

从 n 个不同元素中取出 m 个元素的所有排列的种数，称为从 n 个不同元素中取出 m 个不同元素的排列数，记作 PnmP_n^m 。

排列数计算方法​

Pnm=n(n−1)(n−2)⋅⋯⋅(n−m+1)P_n^m = n(n - 1)(n - 2) \cdot \cdots \cdot (n - m + 1)
当 m = n 时，Pnm=n(n−1)(n−2)⋅⋯⋅2⋅1P_n^m = n(n - 1)(n - 2) \cdot \cdots \cdot 2 \cdot 1， 称为 n 的全排列。
PnnP_n^n = n!，n! 读作 n 的阶乘。
Pnm=n!(n−m)!P_n^m = \frac{n!}{(n - m)!}

第36节 组合与组合数​

组合​

从 n 个不同元素中，任意取出 m 个元素并为一组，称为从 n 个不同元素中取出 m 个元素的一个组合。

组合数​

从 n 个不同元素中取出 m 个元素的所有组合的种数，称为从 n 个不同元素中取出 m 个不同元素的组合数,记作 CnmC_n^m 。

组合数计算方法​

Cnm=PnmPmm=n(n−1)(n−2)⋅⋯⋅(n−m+1)m!C_n^m = \frac{P_n^m}{P_m^m} = \frac{n(n - 1)(n - 2) \cdot \cdots \cdot (n - m + 1)}{m!}
Cnn=Cn0=1C_n^n = C_n^0 = 1
Cnm=Cnn−mC_n^m = C_n^{n - m}

第37节 概率基本概念​

概率​

概率，它反映随机事件出现的可能性大小的量度。

随机试验​

满足下列三个条件的试验称为随机试验

  1. 试验可在相同条件下重复进行；
  2. 试验的可能结果不止一个,且所有可能结果是已知的；
  3. 每次试验哪个结果出现是未知的。

随机事件​

在试验中可能出现也可能不出现的事情称为随机事件。

第38节 事件的关系与运算​

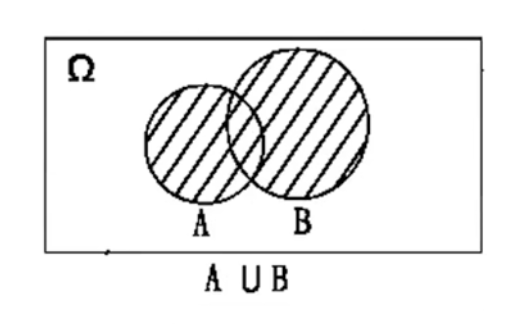
事件的和​

称事件 A 与事件 B 至少有一个发生的事件为 A 与 B 的和事件，简称为和。记为A U B 或 A + B。

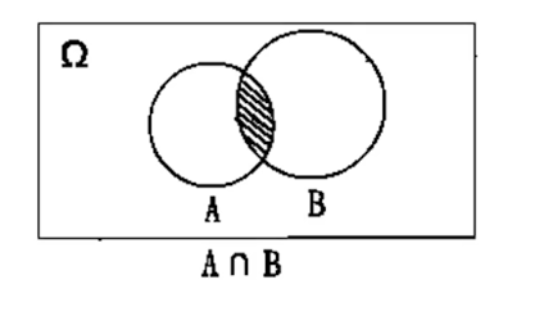
事件的积​

称事件 A 与事件 B 同时发生的事件为 A 与 B 的积事件，简称为积。记为 A ∩ B 或 AB 。

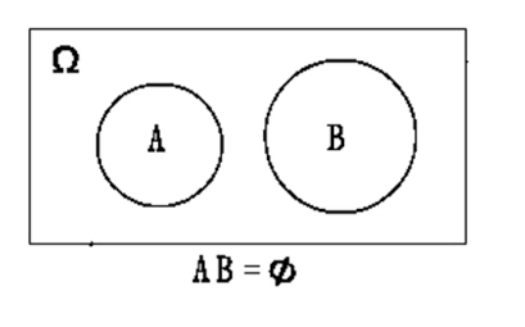
互不相容​

若事件 A 与事件 B 不能同时发生，即 AB = ∅\varnothing ，则称 A 与 B 是互不相容的。

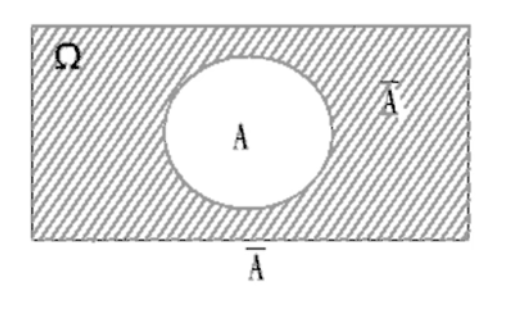
对立事件​

称事件 A 不发生的事件为 A 的对立事件。记为 A‾\overline{A}

第39节 事件的概率及性质​

事件的概率​

所谓事件 A 的概率是指事件 A 发生可能性程度的数值度量，记为 P(A)。显然 0 ≤ P(A) ≤ 1。

概率的性质​

对于任意事件 A、B 有，P(A U B) = P(A) + P(B) -P(AB)
若 A、B 互斥，则 P(A U B) = P(A) + P(B)
对于任意事件 A ，P(A‾\overline{A}) = 1 - P(A)

第40节 平均数、众数和中位数​

算术平均数​

设有 n 个数 x1,x2,⋯xnx_1, x_2, \cdots x_n，称 x1+x2+⋯+xnn\frac{x_1 + x_2 + \cdots + x_n}{n} 为这组数的算术平均数。

几何平均数​

设有 n 个正数 x1,x2,⋯xnx_1, x_2, \cdots x_n ，称 x1⋅x2⋅⋯⋅xnn\sqrt[n]{x_1 \cdot x_2 \cdot \cdots \cdot x_n} 为这组数的几何平均数。

众数​

在 n 个数 x1,x2,⋯xnx_1, x_2, \cdots x_n 中，出现次数最多的数称为众数。

中位数​

将 n 个数 x1,x2,⋯xnx_1, x_2, \cdots x_n 从小到大排列，
当 n 为奇数时，最中间的那个数是中位数，
当 n 为偶数是，处在最中间的两个数的平均数是中位数。