假言推理

假言推理

假言推理就是以一个假言判断做大前提，一个简单判断做小前提。由于假言判断有三种不同的类型，所以，假言推理分为：充分条件假言推理、必要条件假言推理、充要条件假言推理。

充分条件假言推理

例如：

1. 如果天下雨，那么露天的地会湿。
2. 昨天下雨了。
3. 所以，昨天露天的地湿了。

充分条件假言推理的规则

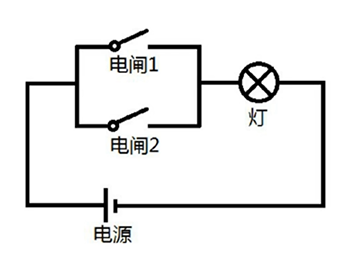
如果电闸 1 接通，那么灯亮。

前件：电闸1接通
后件：灯亮

• 肯定前件，推出肯定后件。（肯前肯后）
• 否定后件，推出否定前件。（否后否前）
• 否定前件，不能否定后件。（否前不能否后）
• 肯定后件，不能肯定前件。（肯后不能肯前）

补充：连锁推理

假言连锁推理又称为纯假言推理，它是由两个或两个以上的假言命题作前提，推出一个假言命题的结论。

如果 P 那么 Q ；
如果 Q 那么 R 。
所以，如果 P 那么 R 。

递推

必要条件假言推理的规则

转换为推的形式，然后参照充分条件假言推理的规则。

只有 P 才 Q。（Q → P）

充要条件假言推理的规则

肯前肯后，否前否后，状态一致。